A Continuous Wire With Current 3a Has a Kink loop
Abstract
When compared with rare-earth coated conductors, magnesium diboride superconducting cables are known to show significant advantages by cost and easy production. However, the inherent difficulty for achieving a significant reduction of their magnetization losses in multifilamentary wires, without degrading the high critical current density that is so characteristic of the monowire, is considered as one of the major drawbacks for their practical use in high power density applications. Being this one of the major markets for superconducting cables, from fundamental principles and computational optimization techniques, in this paper we demonstrate how the embedding of the superconducting filaments into soft-ferromagnetic metastructures can render to their full magnetic decoupling, and therefore, to the maximum reduction of the energy losses that can be achieved without deteriorate the critical current density of the cable. The designed multifilamentary metastructure is made of NbTi coated MgB2 superconducting filaments in a Cu-matrix, serving as a reference for validating our model with actual experimental measurements in monowires and multifilamentary wires. The novelty in our computationally aided multifilamentary wires, is that each one of the filaments is embedded within a thin metastructure made of a soft-ferromagnetic layer and a resistive layer. We have found that for soft-ferromagnetic layers with magnetic permeabilities in the range of \(\mu _{r}=\) 20–100, nearly a full magnetic decoupling between the superconducting filaments can be achieved, leading to efficiencies higher than \(92\%\), and an overall reduction of the AC-losses (including eddy currents at the Cu-matrix) higher than \(50\%\).
Introduction
Despite the enormous progress on the commercialization of high temperature superconducting (SC) wires for high magnetic field and power systems applications1,2,3,4,5, still the so-called low temperature superconductors such as NbTi, Nb\(_{3}\)Sn, and MgB\(_{2}\) with critical temperatures, \(T_{c}\), ranging between \(\sim \)10 K to \(\sim \)39 K, dominate the industrial market6,7,8. If compared with the manufacturing of coated-cuprates conductors, their success is due to their low-cost per unit length, their ease fabrication, and the relative abundance of their base compounds. In this regard, round MgB\(_{2}\) chemically doped wires are of particular importance, not only due to their superior \(T_{c}\) and upper critical field, \(H_{c2}\), but because the powder-in-tube process allows an easy manufacturing of multicore (a.k.a. multifilamentary) wires9,10, as precursors of high-power AC/DC applications such as, power transmission cables11,12,13, rotary machines14,15,16,17, energy-storage devices18, MRI cryogen-free magnets19,20,21, fusion reactors22, and the large scale commercialization of high-current SC links for CERN23,24.
However, the need to operate at temperatures well below sub-cooled liquid nitrogen (65–77 K)25, and the high costs associated with the handling of their energy losses under AC conditions, rise significant issues onto the use of MgB\(_{2}\) wires for power transformers, fault current limiters, and HV-AC cables, capable to function with commercial cryocoolers at sub-cooled LH2-temperatures (15–33 K). Therefore, to enable MgB\(_{2}\) wires tap into the market of AC applications, it results imperative to find meaningful ways to reduce their AC-losses without a detriment of its critical current density, \(J_{c}\). Thus, in this paper we present a novel optimization method applied to realistic designs for multifilamentary MgB\(_{2}\) wires, which aided by the magnetic diverter principle of soft ferromagnetic coatings over superconducting wires26,27,28,29,30,31,32,33,34,35,36,37, can render to the maximum reduction of energy losses than can be achieved by first-physical principles. In this sense, we provide a detailed route for the adequate selection of materials, physical, and engineering dimensions, which in an optimal combination can lead to the fabrication of cost-effective metastructured multifilamentary MgB\(_{2}\) wires for high power density AC applications, that are nowadays accessible only by the use of much more expensive rare-earth coated conductors.
Possible alternatives for the reduction of energy losses in a MgB\(_{2}\) wire
Finding ways for reducing the AC-losses in a SC wire while maintaining its \(J_{c}\) is not trivial, as these are fundamentally constrained by the material properties of the composite, and the robustness of its magnetic flux pinning. Thence, microscopical or macroscopical approaches can be taken, with the first commonly focused on the crystallographic or microstructural properties of the SC compound, despite neither their role on the pairing mechanism leading to the SC phenomenon38,39,40, nor their influence on the vortex pinning dynamics41,42,43,44 are fully understood.
On the other hand, multiple approaches based upon the celebrated Bean's model have arisen45,46, whose success lies on the averaging of all flux pinning forces within a simple magnetostatic scenario. This allows to accurately determine the SC energy losses, with the SC electrical-conductivity known either by intrinsic mechanisms as the one described by the critical state model (CSM)47,48, or by extrinsic measurements of the highly non-linear relationship between the electric field, \(\mathbf{E} \), and the current density, \(\mathbf{J} \), also known as \(\mathbf{E} -\mathbf{J} \) power law49,50. However, it is under the CSM on which it is possible to determine the actual (analytical) physical minimum for the hysteretic AC losses per unit time and volume, L, at least in the case of cylindrical SC wires subjected to external current or magnetic field excitations of frequency \(\omega \) 51,52. This can be calculated then by integration of the local density of power dissipation \((\mathbf{E} \cdot \mathbf{J} )\) over the SC volume \((\Phi )\) as,
$$\begin{aligned} L = \omega \oint _{f.c} dt \int _{\Phi } \mathbf{E} \cdot \mathbf{J} \, d\Phi \, , \end{aligned}$$
(1)
where f.c. denotes a full cycle of the time-varying electromagnetic excitation.
This fact sets a benchmark for which any design of rounded SC wires must be tested53,54,55,56, and from which possible pathways for the reduction of its energy losses can be assessed. Thus, in the CSM only J is constrained by \(J \le J_{c}\), allowing to calculate the minimum energy losses per unit volume of a cylindrical wire of SC cross section area, \(A_{SC}=\pi R_{SC}^{2}\), by57
$$\begin{aligned} L \equiv \dfrac{\mu _{0} I_{c}^{2}}{4\pi ^{2}R_{SC}^{2}}\left[ \left( i_{tr}-\dfrac{i_{tr}^{2}}{2}\right) +\left( 1-i_{tr}\right) \ln \left( 1-i_{tr}\right) \right] , \end{aligned}$$
(2)
with \(i_{tr}\) the ratio between the amplitude of the transport current, \(I_{tr}\), and the critical current, \(I_{c}=J_{c}A_{SC}\).
Then, for determining the total energy losses in realistic MgB\(_{2}\) wires, we have to include the losses from the other materials involved. Thus, we considered three different designs named a monocore, a multicore, and a metastructured wire, with their material properties given in Table 1. The monocore and the multicore designs have been used as benchmark (right-insets at Fig. 1), as the experimental measurement of their AC-losses is known59,60. Ergo, for reproducing these experiments we have used the so-called H-formulation64,65, with our results shown as colour solid lines in Fig. 1.
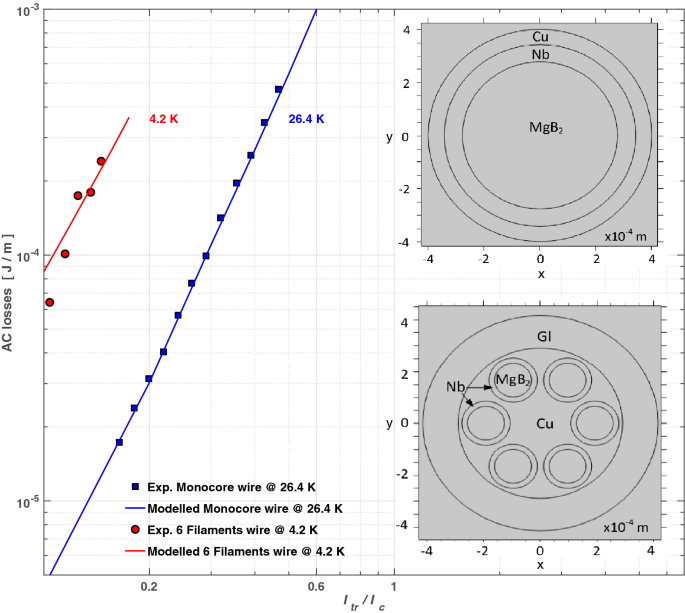
Calculated AC-losses for the MgB\(_{2}\) monocore and multicore wires shown at the right-pane inset. Solid symbols correspond to the experimental measurements at 26.4 K for the monocore wire59, and 4.2 K for the six filaments multifilamentary (multicore) wire60.
Now, there are multiple pathways to be considered when optimizing SC multifilamentary wires. On the one hand, there are extrinsic techniques like chemical doping66,67,68 or irradiation treatments69,70,71, which both can enhance the \(J_{c}\) by improving the flux pinning mechanism, but do not change that the AC-losses will still be dominated by the contributions of the SC filaments and its metallic matrix. On the other hand, extrinsic methods such as the twisting of the filaments can lower the AC-losses, but at the expense of an undesired reduction of \(J_{c}\) 58. Twisting the filaments exploits two physical phenomena not yet well understood, firstly, the angular dependence of the MgB\(_{2}\) pinning properties72,73,74 and, secondly, the possible occurrence of flux cutting effects by the non-perpendicularity between the magnetic field and \(I_{tr}\) 75,76,77,78. The combination of these two phenomena can lead to an "apparent" magnetic decoupling of the SC filaments, apparent in the sense that it can lead to an equivalent reduction of the AC-losses as if no mutual induction would exist. However, there is no general rule in regards to the twisting of MgB\(_{2}\) filaments, as technically speaking, a true magnetic decoupling cannot be achieved unless the mutually induced field between filaments is diverted with the aid of a ferromagnetic material. Hence the advantage of our approach, where the filaments can get truly decoupled by embedding them within a soft ferromagnetic (SFM) sheath, whilst an electrically resistive (RE) layer reduces the losses at its metallic matrix.
The losses by the metallic matrix are due to the strength and change of the magnetic field created by the AC in the MgB\(_{2}\) filaments, whilst the filament losses are due to the \(I_{tr}\) and the self- and mutually-induced magnetization currents appearing in type-II superconductors53,54,55,56. Same happens if other materials with higher thermal conductivity and tensile properties are used for the barrier and outer sheath, such as Nb-Ti, Cu-Nb, or Monel alloys79,80, as they have an almost negligible impact on the total losses of the SC wire58,59,60,81,82. Therefore, the key for achieving a true reduction of the AC-losses lies on finding how to simultaneously lower the magnetically induced currents in the SC filaments, whilst reducing the eddy currents at its metallic matrix. This should be achieved by embedding the SC filaments into ferromagnetic shields as theorized by Majoros, Glowacki and Campbell (MGC) in [83], although contrary to their predictions, a counterintuitive increment on the energy losses has been reported84,85,86,87,88,89,90.
Optimal metastructure for maximal reduction of AC losses
Based on our recent findings on the actual magnetostatic coupling between type-II SC wires and SFM materials37, in this section we explain not only the physical reasons behind the reported increment on the AC losses above mentioned, but also provide a solution pathway for achieving the maximum reduction of energy losses feasible in multifilamentary rounded MgB\(_{2}\) wires. For doing so, in Fig. 2 we present our results for the AC-losses of the considered 6 filaments MgB\(_{2}\) wire under an applied current \(I_{a}=I_{tr} \sin (\omega t)\) at low frequency, e.g., (50 Hz), but where each filament is metastructured with an additional SFM layer within a "resistive" (RE) sheath, whose electrical resistivity is at least a couple of orders greater than the one of the Multicore Matrix (see Table 1). In this sense, if the multicore matrix is made of Cu, with an estimated electrical resistivity of 0.564 \(\mu \Omega \cdot \)cm at 20 K (see Table 1), the RE layer could be made of alloys such as Hastelloy, Inconel, Udimet, or graded AISI austenitic steels91.
Furthermore, it is worth reminding that in conventional power systems encountering excitation frequencies greater than 50–60 Hz is uncommon, but more importantly is to remind that at least within the so-called quasi-steady low frequency regime (below radio frequencies \(\sim \) 20 kHz), the superconductor and the ferromagnetic material can be modelled within the framework of the critical state theory with relatively no differences in he hysteretic losses37,92,93,94. Therefore, not only the standard H-formulation can still be used for determining the distribution of current density inside the superconducting filaments, but the eddy currents to be produced by the SFM and RE layers are not expected to overshadow the hysteretic losses produced by the superconductor, as long as this study is considered within the low frequency regime.
The natural trend for the optimization process can be seen from the right ordinate of the main plot in Fig. 2, i.e., for \(i_{tr}=I_{tr}/I_{c}=1\), where the curves are top to bottom numbered. Starting with the wire with highest losses (1), this curve corresponds to the case where no SFM\RE metastructure is added, therefore consistent with the results and design shown in Fig. 1. Then, the following curves, (2)–(4), correspond to metastructured MgB\(_{2}\) wires with only the SFM filamentary sheaths added. Their purpose is to illustrate the effect of the SFM thickness on the total AC-losses of the MgB\(_{2}\) wire, when a SFM layer of relative magnetic permeability \(\mu _{r}\) coats each of the Nb(Ti)/MgB\(_{2}\) filaments. The trends found with the Nb or the NbTi barrier cases are the same, reason why we call it categorically as Nb(Ti). Also, the selection of this \(\mu _{r}\) is not arbitrary, as a \(\mu _{r}>100\) has serious repercussions on the total AC-losses of the MgB\(_{2}\) wire37. These aspects will be revised later, but for now it suffices to mention that a SFM with \(\mu _{r}=46\) has been chosen, as it has been previously used for fabricating MgB\(_{2}\) monocore wires95,96,97,98. Moreover, it has been assumed as an ideal SFM with a very small coercive force and a sufficiently high saturation field, such that a constant relative magnetic permeability could be assumed. In this sense, although our results stablish a sound benchmark for enabling the fabrication of MgB\(_{2}\) metastructures with minimal AC losses (near the analytical limit), the actual choice and thickness of the SFM must be taken by having into consideration its saturation field, which should be higher than the maximum filed produced by the SC wire.
Hence, it is to be noticed that for a \(30\mu \)m SFM layer, i.e., 1.5 times thicker than the Nb(Ti) barrier (Fig. 2, curve (2)), the total AC-losses at moderate to low transport currents, \(I_{tr}<0.5I_{c}\), are actually greater than the losses for the conventional multicore wire (curve (1)), with lower losses only seen as \(I_{tr}\) approaches \(I_{c}\). However, by reducing the SFM-thickness to equals the one of the barrier (curve (3)), a sooner and stronger reduction of the AC-losses can be seen, with a nearly negligible change for \(i_{tr}\le 0.3\). Then, by further reducing the SFM-thickness to e.g., 10 µm (curve (4)), i.e., half the barrier-thickness, nearly no further reduction on the AC-losses can be observed without the RE-layer. Even if we include the RE-layer (curves 7–9), no further reduction on the AC-losses for \(\delta _{SFM}<15\mu \)m has been found. Therefore, not only choosing a too thick SFM layer could be detrimental, but choosing a thinner SFM layer than the barrier do not implies a continuous reduction on the AC-losses. Thus, our optimization process leads to conclude that an ideal thickness for the SFM sheath would be around the same thickness of the Nb(Ti) barrier, i.e., \(\sim \) 20 µm in our case, with a saturation field greater than 60 mT (Fig. 2c). Nevertheless, we must assess a relative optimization pathway for the barrier's thickness.
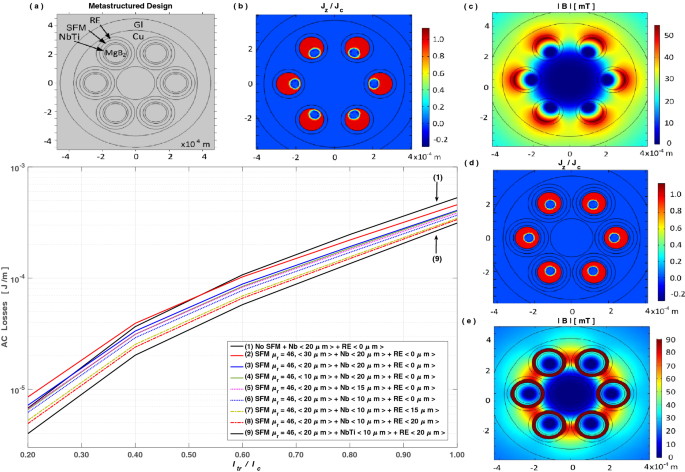
AC losses for multiple (9) MgB\(_{2}\) wires with the thicknesses of the barrier, SFM, and RE layers labelled in quotation marks. (a) shows the metastructured SC wire concept, with the profiles of (b-d) \(J_{z}/J_{c}\) and (c-e) \(|\mathbf{B} |\) displayed for (1) a conventional-wire, and (9) the optimized metastructured-wire, at the peak transport current \(I_{tr} = 0.8 I_{c}\), and with \(J_{c}=1\) GA/m\(^2\) as reference.
The thickness of the Nb(Ti) barrier has been chosen to be \(\pm 10~\upmu \)m the real thickness used for the multicore MgB\(_{2}\) wire in Fig 1 (\(20~\upmu \)m), resulting in a negligible impact on the AC-losses for \(\delta _{Nb(Ti)}\ge 15~\mu \)m (Fig. 2, curves (4) & (5)), and only a slight reduction when it is reduced to \(\delta _{Nb(Ti)}=10~\mu \)m (curve (6)). Therefore, although a significant pathway for reducing the AC-losses at high transport currents in multifilamentary MgB\(_{2}\) wires has been found, yet with an optimal \(20~\upmu \)m SFM layer, the AC-losses reduction is still insignificant at low to moderate \(I_{tr}\). Thus, although we have managed to get a nearly full decoupling of the J-profiles inside the SC filaments (see subplots (b) and (d) at Fig. 2), leading to an actual reduction of the AC-losses for the entire wire, still the advantage of including the SFM sheaths is overshadowed by the eddy currents at the multicore matrix. In this sense, it results vital to understand the physics that leads the reduction of the AC-losses when the SFM is chosen with \(\mu _{r}<100\).
This is no other than the impact of the magnetostatic coupling between the SC and the SFM sheath shown by Fareed and Ruiz in monocore-wires37, whom have demonstrated that no matter the SFM used nor its dimensions, for \(\mu _{r}\gtrsim 100\), the physical coupling between the SC and the SFM leads to a large increment on the electric field outside the SC\SFM metastructure35, but not to a further increment in the density of power losses \(\mathbf{E} \cdot \mathbf{J} \) inside the SC. Moreover, this coupling gets dominated by the factor,
$$\begin{aligned} {\bar{R}}_{\mu 1}=\dfrac{R_{SFM}^{2n}-R_{SC}^{2n}}{\mu _{(-)}^{2} R_{SC}^{2n} - \mu _{(+)}^{2} R_{SFM}^{2n}} \, , \end{aligned}$$
(3)
where \(\mu _{(\pm )}=\mu _{r}\pm 1\), being \(R_{SFM}\) the SFM-sheath outer radius and \(R_{SC}\) its inner radius (outer radius of the Nb(Ti)/MgB\(_{2}\) filament in our case). Thus, following the analytical methods in [37], we have derived the additional contribution for the magnetic vector potential caused by the coupling between a SC\SFM sheathed filament and a line of current inside another SC\SFM filament, i.e.,
$$\begin{aligned} \mathbf{A} _{c,j}(\cdot )= \dfrac{\mu _{0}\mu _{(-)}^{2}}{2\pi }{} \mathbf{J} _{i} \left[ \sum _{n=1}^{\infty } \dfrac{{\bar{R}}_{\mu 1}}{n} \left( \dfrac{r_{j}}{r_{i}}\right) ^{n} \cos (n\phi _{j}) \right] \, . \end{aligned}$$
(4)
Here, \(\mathbf{J} _{i}\) is the current density at an element located at the ith filament (\(i \ne j\)), with \(r_{i}\) the distance between the center of the targeted jth filament and, the element of current inside the magnetically coupled ith filament. Then, the coordinates (\(r_{j},\phi _{j}\)) refer to the polar expansion components of the current elements inside the targeted jth SFM/SC filament. In consequence, the additional contribution on the magnetic vector potential, and therefore on its derived quantities, \(\mathbf{B} =\nabla \times \mathbf{A} \), \(\mathbf{E} =-d\mathbf{A} /dt\), and consequently, \(L\propto \mathbf{E} \cdot \mathbf{J} \), are also governed by the factor, \({\bar{R}}_{\mu 1}\). Therefore, this reveals that for SFM sheaths with \(\mu _{r}>100\), no further enhancement of its "shielding" properties is to be expected for any \(R_{SFM}/R_{SC}\), as for these magnetic permeabilities, \({\bar{R}}_{\mu 1}\) tends to zero [37].
However, in order to balance the sudden increment in the magnetic flux density caused by the SFM, it is already known that near the outer surface of a SC\SFM metastructure, the strength of B and E change rapidly from a much higher value (\(\propto \mu _{r}\)) than the one expected for a bare SC filament37. Therefore, an increment in the eddy currents at the metallic matrix is to be expected, which is likely to increase the overall losses of the MgB\(_{2}\) wire either by an inadequate choice of the SFM \(\mu _{r}\), or by the lack of a RE layer. Thus, in Fig. 2, curves (6)–(8), we show the effect of adding a RE sheath to the metastructured filaments, for which a significant reduction of the AC-losses has been achieved even at low \(i_{tr}\) for \(\delta _{RE}>10~\mu \)m. Likewise, this concept is proved by increasing the barrier's electrical resistivity, e.g., by changing it from Nb to NbTi (Table 1), with which a further AC-losses reduction can be conceived (curve (9)).
Remarkably, when considering other important engineering parameters such as the engineering current density for multicore or metastructured wires, it is to be noted that the designing of metastructured wires can truly result in promising candidates for the next generation of MgB\(_{2}\) based technologies. For instance, if the same critical current density of the superconducting material can be maintained with either of the designs, for instance a \(J_{c} = 1\) GA/m\(^{2}\), leading to a total \(I_{c}\) of 79.6 A per wire (when considering six MgB\(_{2}\) filaments each of 65 µm radius), by increasing the overall radius of the wire from, let's say, 415 µm to 450 µm when including the SFM\RE metastructure, the engineering current density of the wire is decreased by only a 15%. Then, this can be even further reduced to 0%, by simply reducing the thickness of the wire outer coating, i.e., the 80 µm of Glidcop considered in our case, to just 45 µm, what leaves the estimation of the AC losses unaffected. Nevertheless, complementary studies on the tensile properties of the wire should be conducted to determine the optimal and minimum thickness of the outer layer, indistinctly of whether it is the simplified multicore wire or the metastructured wire.
Concluding remarks
By further analysing the impact of the SFM sheath on the AC-losses of SC\SFM\RE metastructured wires (Fig. 3a), starting from a bare SC \((\mu _{r}=1)\), up to a high magnetic permeability \((\mu _{r}=1000)\), i.e., including SFMs such as Ni, NiZn, MnZn, Si, C, and Co ferrites99,100,101, our calculations confirm that for SFM sheaths with \(\mu _{r}>100\), no further reduction of the SC losses can be achieved, but an increment due to eddy currents at the Cu matrix. Thus, Fig. 3b summarizes our main findings, showing how the AC-losses for a SC\SFM\RE wire strongly depends on the SFM selection.
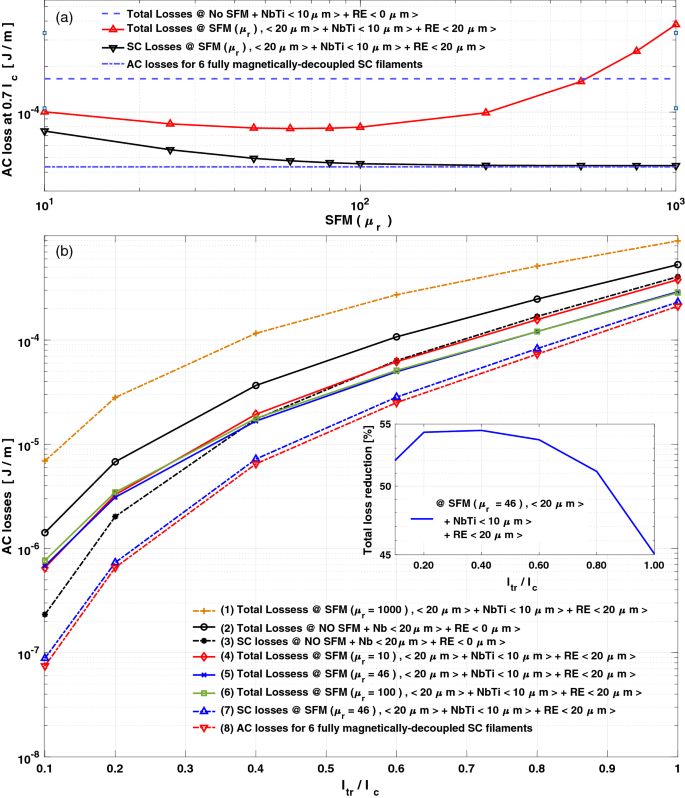
AC-losses for the 6-filaments metastructured wire as a function of (a) the SFM \(\mu _{r}\) at \(I_{tr}=0.7 I_{c}\), and (b) the \(I_{tr}\) condition with different SFM \(\mu _{r}\) options (curves 1–6), leading to the optimal design (5), where a nearly perfect magnetic decoupling between SC filaments is shown (7–8). The inset shows the total AC-loss reduction for the optimal design.
For instance, it explains why when the SFM \(\mu _{r}\) is too high, e.g., \(\mu _{r}=1000\) (curve-(1)), a significant increment on the overall AC-losses is to be observed84,85,86,87,88,89,90. Moreover, with a SFM sheath of \(\mu _{r}\le 100\) and the RE layer, we have proven that the maximum AC-loss reduction (a factor of \(\sim 2\)) predicted by MGC83, can be realized. This is seen by comparing the full (curve-(2)) and the SC (curve-(3)) AC-losses for a conventional MgB\(_{2}\) multifilamentary-wire without the SFM\RE metastructure, with the total losses of the SC\SFM\RE metastructured-wire with a 20 µm SFM sheath of \(\mu _{r}=10\) (curve-(4)), \(\mu _{r}=46\) (curve-(5)), or \(\mu _{r}=100\) (curve-(6)), all embedded within a 20 µm RE layer. Thus, although for low to moderate currents, i.e., for \(I_{tr}\le 0.4I_{c}\), there is a clear reduction of the AC-losses in the order predicted by MGC (see the inset), the wire losses at this regime are mainly dominated by the eddy currents at the Cu-matrix, somehow hiding the achievement of a nearly full magnetic decoupling between the SC filaments. However, the decoupling between the SC filaments becomes clearer when practical values of the current \((I_{tr} > 0.4 I_{c})\) are assumed. For instance, by choosing a SFM with \(\mu _{r}=10\), this metastructured-wire leads to at least the same losses predicted for only the SC filaments in a conventional multifilamentary-wire. In other words, although we still have eddy current losses at the non-SC materials, the total losses including the SC filaments results equivalent to discounting the losses created by the non-SC materials in conventional multifilamentary wires. Moreover, by increasing the \(\mu _{r}\) of the SFM layer to \(\mu _{r}=46\) and then, up to the predicted limit of \(\mu _{r}=100\), it is observed that the total AC-losses of the metastructured-wire result lower than the sole SC losses for the conventional multifilamentary-wires. Therefore, reminding that the SC losses come from the concomitant action between the transport current and the magnetic inductance in the SC filaments56, and neither the transport current losses nor the self-field losses can be reduced as they are bounded by the CSM47, then this can only means the magnetic decoupling between the SC filaments. This is shown by comparing the two bottom curves at Fig. 3b, where the SC losses for the metastructured-wire with SFM \(\mu _{r}=46\) (curve (7)), is contrasted with the analytical solution (Eq. 2) for six fully decoupled SC filaments. Thence, this letter demonstrates that a nearly full decoupling of the SC filaments can be achieved by the right choice of materials within a SC\SFM\RE metastructure, finding a pathway for the maximum reduction of AC-losses envisaged for MgB\(_{2}\) wires.
Data availability
The data that supports the findings of this study are available within the article and from the corresponding author upon reasonable request.
References
-
Molodyk, A. et al. Development and large volume production of extremely high current density YBa2Cu3O7 superconducting wires for fusion. Sci. Rep. 11, 2084 (2021).
-
Jiang, G. et al. Recent development and mass production of high j e 2g-HTS tapes by using thin Hastelloy substrate at Shanghai superconductor technology. Supercond. Sci. Technol.. https://doi.org/10.1088/1361-6668/ab90c4 (2020).
-
Bruzzone, P. et al. High temperature superconductors for fusion magnets. Nucl. Fusion. https://doi.org/10.1088/1741-4326/aad835 (2018).
-
Sundaram, A. et al. 2g HTS wires made on 30 µm thick Hastelloy substrate. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/29/10/104007 (2016).
-
Samoilenkov, S. et al. Customised 2g HTS wire for applications. Supercond. Sci. Technol. 29, 024001. https://doi.org/10.1088/0953-2048/29/2/024001 (2016).
-
Maeda, H. & Yanagisawa, Y. Future prospects for NMR magnets: A perspective. J. Magn. Reson. 306, 80–85. https://doi.org/10.1016/j.jmr.2019.07.011 (2019).
-
Rossi, L. & Tommasini, D. The prospect for accelerator superconducting magnets: HL-LHC and beyond. Rev. Accel. Sci. Technol. 10, 157–187. https://doi.org/10.1142/S1793626819300093 (2019).
-
Parizh, M., Lvovsky, Y. & Sumption, M. Conductors for commercial MRI magnets beyond NBTI: Requirements and challenges. Supercond. Sci. Technol. 30, 014007–014007 (2017).
-
Li, C. et al. Significant improvement in superconducting properties of in situ powder-in-tube MgB2 wires through anthracene doping and heat treatment optimization. Supercond. Sci. Technol. 32, 105004. https://doi.org/10.1088/1361-6668/ab3159 (2019).
-
Kodama, M., Tanaka, K., Okamoto, K., Yamamoto, A. & Ichi Shimoyama, J. Effect of the premixing of MgB2 powder on microstructures and electromagnetic properties in PIT-processed MgB2 wires. Mater. Res. Express. https://doi.org/10.1088/2053-1591/aaeeb8 (2018).
-
Glowacki, B. A. et al. Composite Cu/Fe/MgB2 superconducting wires and MgB2/YSZ/Hastelloy coated conductors for AC and DC applications. Supercond. Sci. Technol. 16, 297–305. https://doi.org/10.1088/0953-2048/16/2/330 (2003).
-
Vysotsky, V. et al. Cryogenic tests of 30 m flexible hybrid energy transfer line with liquid hydrogen and superconducting MgB2 cable. Phys. Procedia67, 189–194, https://doi.org/10.1016/j.phpro.2015.06.033 (2015). Proceedings of the 25th International Cryogenic Engineering Conference and International Cryogenic Materials Conference 2014.
-
Ballarino, A. et al. The best paths project on MgB2 superconducting cables for very high power transmission. IEEE Trans. Appl. Supercond. 26, 1–6 (2016).
-
Kováč, P. et al. Ultra-lightweight superconducting wire based on Mg, B, Ti and Al. Sci. Rep. 8, 11229. https://doi.org/10.1038/s41598-018-29354-1 (2018).
-
Haran, K. S. et al. High power density superconducting rotating machines-development status and technology roadmap. Supercond. Sci. Technol. 30, 123002 (2017).
-
Feddersen, M., Haran, K. S. & Berg, F. AC loss analysis of MgB2-based fully superconducting machines. IOP Conf. Ser. Mater. Sci. Eng.. https://doi.org/10.1088/1757-899x/279/1/012026 (2017).
-
Marino, I. et al. Lightweight MgB2 superconducting 10 MW wind generator. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/29/2/024005 (2016).
-
Morandi, A., Gholizad, B. & Fabbri, M. Design and performance of a 1 MW-5s high temperature superconductor magnetic energy storage system. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/29/1/015014 (2015).
-
Patel, D. et al. Solid cryogen: A cooling system for future MgB2 MRI magnet. Sci. Rep. 7, 43444–43444 (2017).
-
Patel, D. et al. MgB2 for MRI applications: Dual sintering induced performance variations in in situ and IMD processed MgB2 conductors. J. Mater. Chem. C 8, 2507–2516. https://doi.org/10.1039/C9TC06114B (2020).
-
Iwasa, Y. Towards liquid-helium-free, persistent-mode MgB2 MRI magnets: FBML experience. Supercond. Sci. Technol.. https://doi.org/10.1088/1361-6668/aa5fed (2017).
-
Subbotin, M. L. et al. Current status and objectives of modernizing the engineering, physical, and energy infrastructure of the SFT facility for the implementation of the ignitor project. Phys. At. Nucl. 83, 1131–1144 (2020).
-
Konstantopoulou, K., Hurte, J., Retz, P. W. & Ballarino, A. Design optimization and evaluation of the 3 kA MgB2 cable at 4.3 k for the superconducting link project at CERN. Supercond. Sci.Technol.. https://doi.org/10.1088/1361-6668/ab13e7 (2019).
-
Ballarino, A. & Flükiger, R. Status of MgB2 wire and cable applications in Europe. J. Phys. Conf. Ser.. https://doi.org/10.1088/1742-6596/871/1/012098 (2017).
-
Nishimachi, S., Hayakawa, N., Kojima, H., Hanai, M. & Okubo, H. Pressure and temperature dependence of breakdown characteristics of sub-cooled liquid nitrogen. In 2012 Annual Report Conference on Electrical Insulation and Dielectric Phenomena 440–443. https://doi.org/10.1109/CEIDP.2012.6378814 (2012).
-
Glowacki, B. & Majoros, M. Superconducting-magnetic heterostructures: A method of decreasing ac losses and improving critical current density in multifilamentary conductors. J. Phys. Condens. Matter. https://doi.org/10.1088/0953-8984/21/25/254206 (2009).
-
Sanchez, A., Navau, C., Prat-Camps, J. & Chen, D.-X. Antimagnets: Controlling magnetic fields with superconductor-metamaterial hybrids. New J. Phys.. https://doi.org/10.1088/1367-2630/13/9/093034 (2011).
-
Navau, C., Prat-Camps, J., Romero-Isart, O., Cirac, J. I. & Sanchez, A. Long-distance transfer and routing of static magnetic fields. Phys. Rev. Lett. 112, 253901. https://doi.org/10.1103/PhysRevLett.112.253901 (2014).
-
Solovyov, M., Šouc, J. & Gömöry, F. Magnetic cloak for low frequency ac magnetic field. IEEE Trans. Appl. Supercond. 25, 1–5. https://doi.org/10.1109/TASC.2014.2376176 (2015).
-
Genenko, Y. A., Rauh, H. & Kurdi, S. Finite-element simulations of hysteretic alternating current losses in a magnetically coated superconducting tubular wire subject to an oscillating transverse magnetic field. J. Appl. Phys. 117, 243909. https://doi.org/10.1063/1.4922982 (2015).
-
Gömöry, F. et al. Experimental realization of a magnetic cloak. Science 335, 1466–1468. https://doi.org/10.1126/science.1218316 (2012).
-
Gömöry, F., Solovyov, M. & Šouc, J. Magnetization loop modelling for superconducting/ferromagnetic tube of an ac magnetic cloak. Supercond. Sci. Technol. 28, 044001. https://doi.org/10.1088/0953-2048/28/4/044001 (2015).
-
Šouc, J., Solovyov, M. & Gömöry, F. Hiding objects in ac magnetic fields of power grid frequency by two-shell ferromagnetic/superconducting cloak. Appl. Phys. Lett. 109, 033507. https://doi.org/10.1063/1.4959581 (2016).
-
Peña-Roche, J., Genenko, Y. A. & Badía-Majós, A. Magnetic invisibility of the magnetically coated type-II superconductor in partially penetrated state. Appl. Phys. Lett.. https://doi.org/10.1063/1.4961672 (2016).
-
Fareed, M. U., Robert, B. C. & Ruiz, H. S. Electric field and energy losses of rounded superconducting/ferromagnetic heterostructures at self-field conditions. IEEE Trans. Appl. Supercond. 29, 5900705. https://doi.org/10.1109/TASC.2019.2893896 (2019).
-
Baghdadi, M., Ruiz, H. S. & Coombs, T. A. Nature of the low magnetization decay on stacks of second generation superconducting tapes under crossed and rotating magnetic field experiments. Sci. Rep. 8, 1342. https://doi.org/10.1038/s41598-018-19681-8 (2018).
-
Fareed, M. U. & Ruiz, H. S. Critical state theory for the magnetic coupling between soft ferromagnetic materials and type-II superconductors. Materials 14, 6204. https://doi.org/10.3390/ma14206204 (2021).
-
Schachinger, E., Tu, J. J. & Carbotte, J. P. Angle-resolved photoemission spectroscopy and optical renormalizations: Phonons or spin fluctuations. Phys. Rev. B 67, 214508. https://doi.org/10.1103/PhysRevB.67.214508 (2003).
-
Ruiz, H. S. & Badía-Majós, A. Nature of the nodal kink in angle-resolved photoemission spectra of cuprate superconductors. Phys. Rev. B 79, 054528. https://doi.org/10.1103/PhysRevB.79.054528 (2009).
-
Novko, D., Caruso, F., Draxl, C. & Cappelluti, E. Ultrafast hot phonon dynamics in MgB2 driven by anisotropic electron–phonon coupling. Phys. Rev. Lett.. https://doi.org/10.1103/PhysRevLett.124.077001 (2020).
-
Bhagurkar, A. G. et al. High trapped fields in c-doped MgB2 bulk superconductors fabricated by infiltration and growth process. Sci. Rep. 8, 1–12 (2018).
-
Takahashi, Y., Naito, T. & Fujishiro, H. Vortex pinning properties and microstructure of MgB2 heavily doped with titanium group elements. Supercond. Sci. Technol. 30 https://doi.org/10.1088/1361-6668/aa91ed (2017).
-
Liu, H. et al. Improved superconducting properties for multifilament graphene-doped MgB2 wires by an internal mg diffusion process. Mater. Lett. 227, 305–307 (2018).
-
Zou, X. et al. Preparation of MgB2 superconducting wires by the rapid heating and quenching method. Mater. Lett. 244, 111–114 (2019).
-
Bean, C. P. Magnetization of hard superconductors. Phys. Rev. Lett. 8, 250–253. https://doi.org/10.1103/PhysRevLett.8.250 (1962).
-
Bean, C. P. Magnetization of high-field superconductors. Rev. Mod. Phys. 36, 31–39. https://doi.org/10.1103/RevModPhys.36.31 (1964).
-
Badía-Majós, A., López, C. & Ruiz, H. S. General critical states in type-II superconductors. Phys. Rev. B 80, 144509. https://doi.org/10.1103/PhysRevB.80.144509 (2009).
-
Ruiz, H. S. & Badía-Majós, A. Smooth double critical state theory for type-II superconductors. Supercond. Sci. Technol. 23, 105007 (2010).
-
Zhang, X., Zhong, Z., Ruiz, H. S., Geng, J. & Coombs, T. A. General approach for the determination of the magneto-angular dependence of the critical current of YBCO coated conductors. Supercond. Sci. Technol.. https://doi.org/10.1088/1361-6668/30/2/025010 (2017).
-
Robert, B. C., Fareed, M. U. & Ruiz, H. S. How to choose the superconducting material law for the modelling of 2g-HTS coils. Materials 12, 2679. https://doi.org/10.3390/ma12172679 (2019).
-
Gurevich, A. V., Mints, R. G. & Rakhmanov, A. L. Physics of Composite Superconductors (Begell House, New York, 1997).
-
Ruiz Rondan, H. Material Laws and Numerical Methods in Applied Superconductivity (University of Zaragoza Press, Zaragoza, 2013).
-
Robert, B. C. & Ruiz, H. S. Electromagnetic response of dc type-II superconducting wires under oscillating magnetic excitations. IEEE Trans. Appl. Supercond. 28, 8200905. https://doi.org/10.1109/TASC.2017.2668060 (2018).
-
Robert, B. C. & Ruiz, H. S. Magnetization profiles of ac type-II superconducting wires exposed to DC magnetic fields. IEEE Trans. Appl. Supercond. 28, 8200805. https://doi.org/10.1109/TASC.2018.2794138 (2018).
-
Ruiz, H. S. & Badía-Majós, A. Exotic magnetic response of superconducting wires subject to synchronous and asynchronous oscillating excitations. J. Appl. Phys. 113, 193906. https://doi.org/10.1063/1.4804931 (2013).
-
Ruiz, H. S., Badía-Majós, A., Genenko, Y. A., Rauh, H. & Yampolskii, S. V. Superconducting wire subject to synchronous oscillating excitations: Power dissipation, magnetic response, and low-pass filtering. Appl. Phys. Lett. 100, 112602. https://doi.org/10.1063/1.3693614 (2012).
-
Norris, W. T. Calculation of hysteresis losses in hard superconductors carrying AC: Isolated conductors and edges of thin sheets. J. Phys. D Appl. Phys. 3, 489 (1970).
-
Kováč, P. et al. Filamentary MgB2 wires with low magnetization ac losses. IEEE Trans. Appl. Supercond. 26, 1–5 (2016).
-
Kajikawa, K. et al. AC losses in monofilamentary MgB2 round wire carrying alternating transport currents. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/23/4/045026 (2010).
-
Majoros, M. et al. Ac transport current and applied magnetic field losses in MgB2 multifilamentary strands with non-magnetic sheath materials. AIP Conf. Proc. 986, 388–395. https://doi.org/10.1063/1.2900372 (2008).
-
Majoros, M., Glowacki, B., Campbell, A., Apperley, M. & Darmann, F. Transport ac losses in (bi, pb)srcacuo-2223/ag multifilamentary tapes with different filament arrangements. Physica C Supercond. 323, 125–136 (1999).
-
Holúbek, T., Kováč, P., Takács, S., Hušek, I. & Melišek, T. Current sharing and the stability of composite MgB2 superconductors. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/21/6/065013 (2008).
-
Polák, M. et al. Ac losses and transverse resistivity in filamentary MgB2 tape with Ti barriers. Physica C 471, 389–394. https://doi.org/10.1016/j.physc.2011.04.004 (2011).
-
Robert, B. C., Fareed, M. U. & Ruiz, H. S. Flux front dynamics and energy losses of magnetically anisotropic 2g-HTS pancake coils under prospective winding deformations. Eng. Res. Express. https://doi.org/10.1088/2631-8695/ab42e6 (2019).
-
Baghdadi, M., Ruiz, H. S. & Coombs, T. A. Crossed-magnetic-field experiments on stacked second generation superconducting tapes: Reduction of the demagnetization effects. Appl. Phys. Lett. 104, 232602. https://doi.org/10.1063/1.4879263 (2014).
-
Yang, Y., Sumption, M. D. & Collings, E. W. Influence of metal diboride and Dy2O3 additions on microstructure and properties of MgB2 fabricated at high temperatures and under pressure. Sci. Rep. 6, 29306–29306 (2016).
-
Zhao, Y. et al. CrB2 doping effects on critical current density and flux pinning of MgB2. IEEE Trans. Appl. Supercond. 29, 1–5 (2019).
-
Jirsa, M. et al. Flux pinning and microstructure of a bulk MgB2 doped with diverse additives. Supercond. Sci. Technol. 33, 94007 (2020).
-
Bugoslavsky, Y. et al. Enhancement of the high-magnetic-field critical current density of superconducting MgB2 by proton irradiation. Nature (London) 411, 561–563 (2001).
-
Eisterer, M. et al. Neutron irradiation of MgB2 bulk superconductors. Supercond. Sci. Technol. 15, L9–L12 (2002).
-
Jung, S.-G. et al. Influence of carbon–ion irradiation on the superconducting critical properties of MgB2 thin films. Supercond. Sci. Technol. 32, 25006 (2019).
-
de Lima, O. F., Cardoso, C. A., Ribeiro, R. A., Avila, M. A. & Coelho, A. A. Angular dependence of the bulk nucleation field \({H}_{c2}\) of aligned MgB2 crystallites. Phys. Rev. B. https://doi.org/10.1103/PhysRevB.64.144517 (2001).
-
Jang, D.-J. et al. Angular dependences of the motion of the anisotropic flux line lattice and the peak effect in MgB2. Supercond. Sci. Technol. 21, 125004 (2008).
-
Eisterer, M., Häßler, W. & Kováč, P. Critical currents in weakly textured MgB2: Nonlinear transport in anisotropic heterogeneous media. Phys. Rev. B. https://doi.org/10.1103/PhysRevB.80.174516 (2009).
-
Clem, J. R. Theory of flux cutting and flux transport at the critical current of a type-II superconducting cylindrical wire. Phys. Rev. B 83, 214511. https://doi.org/10.1103/PhysRevB.83.214511 (2011).
-
Ruiz, H. S., Badía-Majós, A. & López, C. Material laws and related uncommon phenomena in the electromagnetic response of type-II superconductors in longitudinal geometry. Supercond. Sci. Technol. 24, 115005. https://doi.org/10.1088/0953-2048/24/11/115005 (2011).
-
Ruiz, H. S., López, C. & Badía-Majós, A. Inversion mechanism for the transport current in type-II superconductors. Phys. Rev. B 83, 014506. https://doi.org/10.1103/PhysRevB.83.014506 (2011).
-
Olutaş, M., Kiliç, A., Kiliç, K. & Altinkök, A. Flux motion and isotropic effects in MgB2 near the critical temperature. Eur. Phys. J. B Condens. Matter Phys. 85, 1–11 (2012).
-
Tomsic, M. et al. Development of magnesium diboride (MgB2) wires and magnets using in situ strand fabrication method. Physica C Supercond. 456, 203–208 (2007).
-
Sun, Y. et al. Mechanical and superconducting properties of 6-filament MgB2 wires reinforced by Cu, Cu–Nb and NbTi. Physica C Supercond. 477, 56–62 (2012).
-
Kováč, J., Šouc, J., Kováč, P. & Hušek, I. Magnetization AC losses in MgB2 wires made by IMD process. Supercond. Sci. Technol.. https://doi.org/10.1088/0953-2048/28/1/015013 (2015).
-
Deniskina, N. V. & Getman, F. I. Magnetic screening as a possible way to decrease transport ac losses in multifilamentary superconductors—basic theoretical considerations. IEEE Trans. Appl. Supercond. 26, 1–3. https://doi.org/10.1109/TASC.2015.2501098 (2016).
-
Majoros, M., Glowacki, B. & Campbell, A. Magnetic screening as a possible way to decrease transport ac losses in multifilamentary superconductors—basic theoretical considerations. Physica C 334, 129–140. https://doi.org/10.1016/S0921-4534(00)00276-8 (2000).
-
Kováč, P. et al. Magnetic interaction of an iron sheath with a superconductor. Supercond. Sci. Technol. 16, 1195. https://doi.org/10.1088/0953-2048/16/10/312 (2003).
-
Horvat, J., Soltanian, S. & Yeoh, W. K. The relevance of the self-field for the 'peak effect' in the transport \(j_{c}(h)\) of iron-sheathed MgB2 wires. Supercond. Sci. Technol. 18, 682. https://doi.org/10.1088/0953-2048/18/5/017 (2005).
-
Young, E., Bianchetti, M., Grasso, G. & Yang, Y. Characteristics of ac loss in multifilamentary MgB2 tapes. IEEE Trans. Appl. Supercond. 17, 2945–2948. https://doi.org/10.1109/TASC.2007.899094 (2007).
-
Majoros, M. et al. Ac losses in MgB2 multifilamentary strands with magnetic and non-magnetic sheath materials. IEEE Trans. Appl. Supercond. 19, 3106–3109. https://doi.org/10.1109/TASC.2009.2019107 (2009).
-
Nikulshin, Y. et al. Monel contribution to ac losses in MgB2 wires in frequencies up to 18 khz. IEEE Trans. Appl. Supercond. 28, 1–6. https://doi.org/10.1109/TASC.2018.2841926 (2018).
-
Nikulshin, Y., Yeshurun, Y. & Wolfus, S. Effect of magnetic sheath on filament ac losses and current distribution in MgB2 superconducting wires: Numerical analysis. Supercond. Sci. Technol. 32, 75007. https://doi.org/10.1088/1361-6668/ab13d9 (2019).
-
Xi, J. et al. Experimental test and analysis of ac losses in multifilamentary MgB2 wire. IEEE Trans. Appl. Supercond. 29, 1–5. https://doi.org/10.1109/TASC.2019.2903924 (2019).
-
Fickett, F. R. Electric properties of materials and their measurement at low temperatures. Technical Report, U.S. Department of Commerce, National Bureau of Standards (1982). NBS Technical Note 1053.
-
Fiorillo, F. & Beatrice, C. Energy losses in soft magnets from dc to radiofrequencies: Theory and experiment. J. Supercond. Novel Magn. 24, 559–566. https://doi.org/10.1007/s10948-010-1000-9 (2011).
-
Coffey, M. W. High-frequency linear response of anisotropic type-II superconductors in the mixed state. Phys. Rev. B 47, 12284–12287. https://doi.org/10.1103/PhysRevB.47.12284 (1993).
-
Prozorov, R., Shaulov, A., Wolfus, Y. & Yeshurun, Y. Frequency dependence of the local ac magnetic response in type-II superconductors. Phys. Rev. B 52, 12541–12544. https://doi.org/10.1103/PhysRevB.52.12541 (1995).
-
Pan, A. V., Zhou, S., Liu, H. & Dou, S. Direct visualization of iron sheath shielding effects in MgB2 superconducting wires. Supercond. Sci. Technol. 16, L33–L36. https://doi.org/10.1088/0953-2048/16/10/101 (2003).
-
Pan, A. V. & Dou, S. Overcritical state in superconducting round wires sheathed by iron. J. Appl. Phys. 96, 1146–1153. https://doi.org/10.1063/1.1763224 (2004).
-
Genenko, Y. A., Yampolskii, S. V. & Pan, A. V. Virgin magnetization of a magnetically shielded superconductor wire: Theory and experiment. Appl. Phys. Lett. 84, 3921–3923. https://doi.org/10.1063/1.1741036 (2004).
-
Yampolskii, S. V. & Genenko, Y. A. Entry of magnetic flux into a magnetically shielded type-II superconductor filament. Phys. Rev. B. https://doi.org/10.1103/PhysRevB.71.134519 (2005).
-
Williams, B. Power Electronics: Devices, Drivers, Applications, and Passive Components (McGraw-Hill, New York, 1992).
-
DOD. Military handbook. grounding, bonding, and shielding for electronic equipments and facilities. Technical Report, Department of Defense, Washington, DC. (1987). MIL-HDBK-419A.
-
Solymar, L., Solymar, P., Walsh, D. & Walsh, B. Lectures on the Electrical Properties of Materials. Oxford Science Publications (Oxford University Press, Oxford, 1988).
Acknowledgements
This work was supported by the UK Research and Innovation, Engineering and Physical Sciences Research Council (EPSRC), through the grant Ref. EP/S025707/1 led by H.S.R. All authors acknowledge the use of the High Performance Computing facility ALICE at the University of Leicester.
Author information
Authors and Affiliations
Contributions
M.K. and H.S.R have equally contributed in the paper conception, writing, method, and analysis of results. All authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Kapolka, M., Ruiz, H.S. Maximum reduction of energy losses in multicore MgB2 wires by metastructured soft-ferromagnetic coatings. Sci Rep 12, 7030 (2022). https://doi.org/10.1038/s41598-022-10728-5
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1038/s41598-022-10728-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
rothwellinhat1968.blogspot.com
Source: https://www.nature.com/articles/s41598-022-10728-5
0 Response to "A Continuous Wire With Current 3a Has a Kink loop"
Post a Comment